Too Young

今天做了一套模拟题，成功爆20。

这套题出题人全程暴力%，~~今朝笑话讲的好，——。~~

但我笑着笑着就笑不出来了。

然后就爆20了。

在众多毒瘤题的包围下来一套简单的小水题，可以愉悦身心、增加信心…

这么简单地一套题相信大家都已经轻松AK了，不过CSP-S可就不一定也这么水了，希望大家在CSP-S的第一年也能RP++，虐场快乐

——出题人

我：？

这是第一题，后两道太NaN了

题目

大学选课真的是一件很苦恼的事呢！

Marco：“我要两年毕业！我要选尽量多的学分！这些课统统选上！”

长者：“你啊，Too Young！你看看作业量，你做的完吗？”

Marco（笑容逐渐消失.gif）：”那可咋整啊?“

长者："还能咋整？退课呗！“

已知 Marco 选了 $N(1 \leq N \leq 500)$ 门课，每门课有学分 $w_i$ ，劳累度 $v_i$ 和挂科概率 $p_i$ ；

其中， $w_i$ 为 $[1,5]$ 范围内的一个正整数， $v_i$ 是 int 范围内正整数， $p_i$ 是 $[0,1]$ 范围内小数；

现在 Marco 想退掉某些课使得自己的劳累度尽量小，但是，如果 Marco 的学分总数达不到给定的 $MINX$ ，他会被退学。

Marco想知道，在期望学分大于等于 $MINX$ 的情况下，他的最小劳累度是多少。

注意：如果一门课挂科，Marco 将付出 $v_i$ 的劳累度但是无法获得相应学分；否则，Marco 将付出 $v_i$ 的劳累度并收获 $w_i$ 的学分。

输入格式

第一行一个正整数 $N$ 表示课程数量

接下来 $N$ 行，每行空格分开的 $3$ 个数 $w_i,v_i$ 和 $p_i$ ，含义如题面所述

最后一行一个正整数 $MINX$ 表示所需最小学分。

输出格式

一行一个正整数表示最小劳累度。

数据范围

本题共 10 个测试点，每个测试点 10 分。

对于 $10\%$ 的数据， $1 \leq N \leq 10$

对于 $30\%$ 的数据， $1 \leq N \leq 20$

对于另外 $20\%$ 的数据， $p_i=0$

对于 $100\%$ 的数据，

$1 \leq N \leq 500$ ，

$w_i$ 是正整数且 $1 \leq wi \leq 5$ ，

$p_i$ 最多包含 $2$ 位小数且 $0 \leq pi \leq 1$ ，

$v_i$ 是 int 范围内正整数.

保证全选的情况下 Marco 不会被退学。

输出时每行末尾的多余空格，不影响答案正确性

样例输入

样例输出

样例解释

只选择第 $2$ 门课，期望学分为 $2*0.5=1$ 分，劳累程度为 1

思路

最开始想的是f[i][j]表示考虑到了第i门课，劳累度为j时得的最大分数

然后发现j的范围太大。。。

又想着拿f[i][j]表示考虑到第i门课，期望得分j的最小劳累度

但期望得分是小数啊！！

然后瞎鸡儿写了个n<20,dfs，n>20,瞎Dp

此题爆零。

赛后看题解：

e9b58.png)

好，好的！

还有一个卡精度的问题。

借一下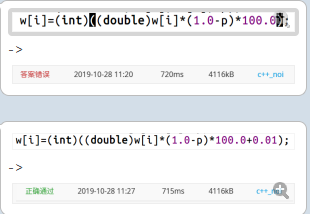16a5d.png)

啥？？

然后我发现

100 - p * 100也是不行的

加上0.01或者round(100 - p * 100)都能过？？

算了算了，以后记得用round。

代码

就这么几行。。。

#include <cstdio>
#include <algorithm>
#include <cmath>

const int MAXN = 505;

int w[MAXN], v[MAXN];
long long f[MAXN * MAXN];
int n;
int minx;
int maxW = 0;
long long ans = (1ll<<60ll);

int main (void) {
	freopen("young.in", "r", stdin);
	freopen("young.out", "w", stdout);
	scanf("%d", &n);
	for (int i = 1; i <= n; ++i) {
		double p;
		scanf("%d%d", w + i, v + i);
		scanf("%lf", &p);
		w[i] *= round(100 - p * 100);
		maxW += w[i];
	}
	scanf("%d", &minx);
	minx *= 100;
	for (int i = 1; i <= maxW; ++i) {
		f[i] = (1ll<<60ll);
	}
	int sum = 0;
	for (int i = 1; i <= n; ++i) {
		sum += w[i];
		for (int j = sum; j >= w[i]; --j) {
			f[j] = std::min(f[j], f[j - w[i]] + v[i]);
		}
	}
	for (int i = minx; i <= sum; ++i) {
		ans = std::min(ans, f[i]);
	}
	printf("%lld\n", ans);
	return 0;
}